在生产环境的推荐系统中部署Contextual bandit (LinUCB)算法的经验和陷阱

一、推荐冷启动问题

当新用户或新物品进入内容平台时，就会出现冷启动（Cold Start）问题。比如，内容平台新发布的短视频、电商平台新上架的商品、媒体平台新发布的新闻等等，这些新的内容之前从未获得过曝光，从未有用户对它们表示过感兴趣或不感兴趣。推荐系统该如何决定这些内容是否需要被推荐，以及推荐给哪些合适的用户？这就是推荐冷启动问题。

相对于冷启动的物品（泛指商品、新闻、作品等需要被推荐的内容），非冷启动物品因为以及获得了大量的曝光，推荐系统收集了用户对它们的一些交互行为，这些行为显式或隐式反馈了用户对这些物品的兴趣。基于这些行为日志，推荐系统可以用比较成熟的推荐算法来对这些物品进行个性化的推荐，让合适的物品被呈现给合适的用户。

为什么需要冷启动方案，原因如下：

目前的召回、粗排、精排算法对新物品、新用户不友好
新物品很大程度上，会被模型”低估”
冷启动问题不可逃避
- 处理不好会影响内容创造者的积极性，进而影响平台生态的健康发展

冷启动物品由于缺乏或暂未获得足够丰富的用户交互行为日志，给推荐算法带来了不小的挑战。目前冷启动推荐大致有以下几种思路：

基于物品的属性数据（side information），比如利用商品的类目、品牌等信息；文章的作者、类别、关键词、摘要等。
基于其他领域的知识，比如领域知识图谱等
使用元学习（meta learning）的方法
基于试错的Contextual Bandit的方法

本文主要关注基于Contextual Bandit的方法，具体地，我们会介绍LinUcb算法的原理、生产环境部署的基础设施架构、算法框架、工程实现时的注意事项、特征设计的陷阱、算法超参数的选择等内容。

二、LinUCB算法

先不考虑用户的情况，每一个新的物品被推荐出去后，所能获得的收益是不一样的。这里的收益根据推荐系统的目标来定义，比如不同的行为获得不同的收益，拿电商平台来说，点击行为获得的收益假设是0.5，加购物车的行为获得的收益可以定义为0.8，下单购买的行为收益可以定义为1.0。那么，推荐系统在每一次用户到达时该如何决定推荐哪个物品才能获得长期累积的最大收益呢？这其实就是一个MAB（Multi-Arm Bandit）问题。

假设系统记录了每个物品被推荐的次数 $n_i$ 和获得的收益，我们就可以计算出每个物品被推荐后所能获得的收益均值 $\hat\mu_i$，那之后是不是就可以一直选择收益均值大的物品推荐，而不再推荐收益均值小的物品呢？其实是不可以的，因为根据大数定律，只有在实验次数足够多时，统计得到的均值才接近于随机变量的真实均值。假设有一个物品只被推荐了一两次，这个时候计算出的均值是不准确的，我们不能据此就判断下次推荐这个物品时还能获得跟当前计算出的均值相当的收益。那该怎么办呢？假设物品的收益服从正态分布，那么除了均值，我们还可以计算每个物品收益的方差或标准差。方差越小，表示均值越置信；反之，均值越不置信。这样我们就计算出了每个物品的收益均值，以及置信区间。UCB（Upper Confidence Bound）算法就是根据估算的置信区间上界来选择下次需要被推荐的物品。具体计算公式如下：

$\hat\mu_i + \sqrt{\frac{2ln(n)}{n_i}}$

其中，$n$为总的推荐次数， $n_i$为物品 $i$ 被推荐的次数。可以看出，某物品被推荐的次数越多，上式第二项就越小，也就是其均值更有置信度，这个时候算法偏向于利用（exploit）已经获得的知识（收益均值）；相反，如果某物品被推荐的次数越少，上式第二项就越大，从而更有机会被推荐，这个时候算法偏向于探索（explore）新的曝光量较少的物品，以期望能够发现未来收益率更高的优质物品。在推荐系统中，Exploitation-Exploration平衡是一个重要的机制。

可以看出，上述推荐物品的过程没有充分利用推荐场景的上下文信息，为所有用户选择展现物品的策略都是相同的，忽略了用户作为一个个活生生的个体本身的兴趣点、偏好、购买力等因素都是不同的，因而，同一个物品在不同的用户、不同的情景下接受程度是不同的。故在实际的推荐系统中，我们还会把用户和场景的特征考虑进去，把这样的算法称之为Contextual Bandit算法。

LinUCB算法就是一个经典的Contextual Bandit算法，它假设物品的收益由一个线性模型决定，模型的特征编码了用户信息、上下文场景信息、用户-物品交叉的信息等，其原理类似于上述UCB算法。关于LinUCB算法原理的详细内容请参考这篇很火爆的文章《Contextual Bandit算法在推荐系统中的实现及应用》，这里不再赘述。

LinUCB算法需要实时收集被推荐物品的收益，以便据此决定下一步的推荐策略，因此，LinUCB算法是一个在线学习（online learning）模型，但它与传统的在线学习模型（如ftrl、ODL等）又有不同的地方，主要有两点区别：

每个arm（物品）学习一个独立的模型（context只需要包含user-side和user-arm interaction的特征，不需要包含arm-side特征）；而传统在线学习为整个业务场景学习一个统一的模型
传统的在线学习采用贪心策略，尽最大可能利用已学到的知识，没有exploration机制（贪心策略通常情况下都不是最优的）；LinUCB则有较完善的E&E机制，关注长期整体收益

在生产环境部署在线学习模型并不是一件容易的事情，涉及到的基础设施和工程链路都比较复杂，下面就带大家看一种可行的方案。

三、算法框架

根据是否在Arm之间共享部分参数，LinUCB可以分为不共享参数的Disjoint版本和共享参数的Hybrid版本。下面我们以Disjoint版本为例，介绍一下算法框架和工程实现相关的内容。

Disjoint版的LinUCB本身很简单，算法伪代码如上图，其中第0行到第11行需要在推荐服务内部实现，这部分包括了模型参数同步、模型预测、Exploitation-Exploration机制的实现、实时特征的记录和存储等；第2行、第11行到第13行需要在一个实时计算平台内部实现，比如可以基于flink或storm来实现。实时计算平台与推荐服务之间需要有分布式存储系统来同步模型参数和实时样本特征，可选的分布式存储系统包括Hologres、Redis等，推荐使用Hologres来实现，因为其存储的每一条记录可以分为多个字段结构化存储，类似于数据库系统。整体框架图如下：

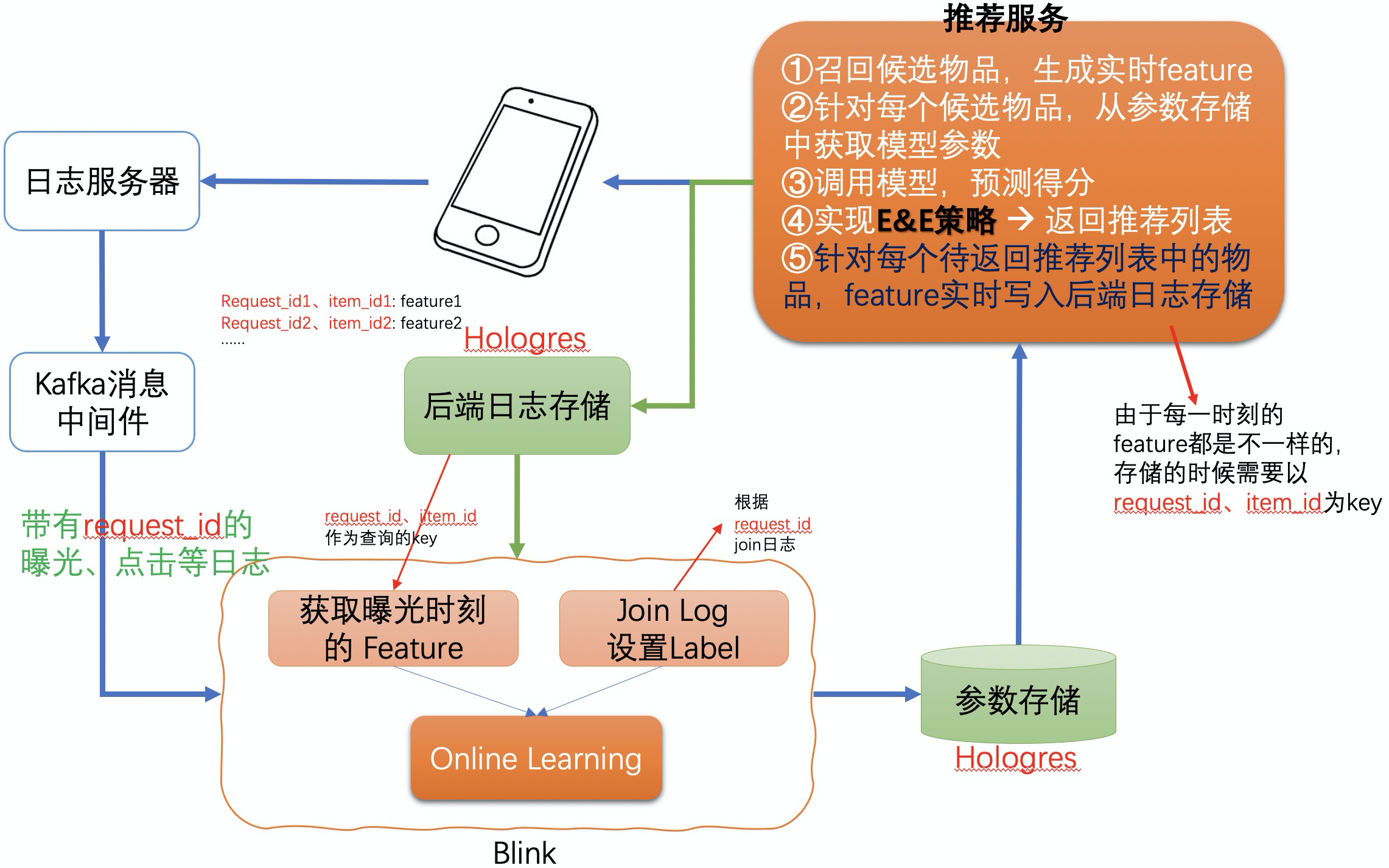
因为用户看到推荐物品的列表后需要间隔一段时间才能产生交互行为，所以模型训练过程中针对曝光样本需要在内存中存储一段时间，等待产生收益的行为日志到达。Flink/Blink系统比较容易实现这个逻辑，可以基于KeyedProcessFunction、OnTimer接口与Flink State配合来实现。这里需要特别设计一下代码逻辑，保证每个曝光样本都能等待足够长的时间，同时又能比较集中地输出更新后的模型参数。

Hybrid版的LinUCB算法相对比较复杂，伪代码如上图。相对于disjoint版本的算法，hybrid版的算法不仅计算公式更加复杂，而且因为多了一组全局的共享参数，给工程实现带来了不小的挑战。因为Flink的State是不能夸worker共享的，所以全局共享参数需要使用外部存储，在分布式环境下全局共享参数会面临可能的读写冲突问题，要正确实现并不容易。

四、特征工程

1. 谨防哑变量陷阱

“A trap is only a trap if you don’t know about it.”

深度学习大大简化了特征工程需要处理的内容，然而LinUCB算法是一个线性模型，因而要想获得比较好的推荐效果，就需要精心设计特征，仔细设计的特征变换可以让线性模型达成相当于在原始特征上训练非线性模型的效果。

在深度学习时代，对于类别特征，大家习惯使用one-hot编码做特征变换，然而我需要特别提醒大家注意的是，在一个线性模型中使用one-hot编码可能会掉入“哑变量陷阱（Dummy variable trap）”中。比如对于用户的性别这个变量，one-hot编码通常会创建两个特征：is_male、is_female，在线性模型中使用这样的两个特征就会面临“多重共线性（multicollinear）”问题，也就是两个或多个特征之间是高度相关的，其中一个变量的值能够由其他变量的值预测出来。假设模型仅使用性别这一个特征，那么有如下等式：

$\begin{equation} y = b_0 + b_1 * is\_male + b_2 * is\_female \end{equation}$

由于is_male、is_female不能同时为1，它们之间有如下关系：

$is\_male + is\_female = 1$

也就是 $is_male = 1 - is_female$，代入公式(1)，得：

$\begin{equation} y = (b_0 + b_1) +（b_2 - b_1) * is\_female \end{equation}$

由此可见，其实模型并不需要两个互相依赖的特征变量。

哑变量陷阱会导致特征维数变多，影响模型求解效率和参数同步的代价。更严重的是，哑变量陷阱会让模型求解过程中面临非满秩矩阵求逆的难题，对回归参数估计带来严重影响。随着多重共线性程度的提高，参数方差会急剧上升到很大的水平，理论上使最小二乘估计的有效性、可靠性和价值都收到影响，实践中参数估计的稳定性和可靠程度下降。

2. 特征设计需要考虑模型的归纳偏置

假设一个二值特征的取值只有0和1两种，如出生地是否为中国，那么有两种设计特征的思路：第一种是出生地在中国的人特征值为1，即is_born_in_china；第二种是出生地不在中国的人特征值为1，即is_not_born_in_china。如果训练集是固定的，那么最终模型的效果可能是一样的，只是学到的特征权重刚刚相反而已。然而，在冷启动物品的推荐场景，哪种设计更好一些呢？推荐结果本身就在改变系统未来能收集到的数据的分布，是一个动态决策的过程，这跟那一个固定的数据集训练模型是有本质区别的。

如果你仔细看disjoint版本的linucb算法，你就会发现算法对一个全新的物品预测分数：

$p_{disjoint} = \alpha \sqrt{x^Tx}$

其中，$\alpha$ 是超参数，决定模型是偏向于探索还是偏向于利用。全新物品的预测分数就等于其特征向量的长度（2范数）。

同样，hybrid版本的linucb算法对一个全新的物品的预测分数为：

$p_{hybrid} = \alpha \sqrt{z^Tz + x^Tx}$

可见全新物品的预测值只跟特征向量的内积有关，内积越大，预测值越大。

特征设计如果能够使得特征向量的长度越大，越能够代表该物品容易被用户接受，更符合业务sense，这样的设计就是一个好的设计，反之，就是一个糟糕的设计。毕竟，对于一个全新的物品，其特征向量长度越大越容易被LinUCB算法选择为推荐标的物。比如，一个相亲平台我们应该设计满足用户征友条件的特征，如年龄是否匹配‘is_age_satisfied’，而不要设计相反含义的特征‘is_age_not_satisfied’，这样我们在推荐一个全新的用户时，推荐逻辑比较符合预期；相反的话就可能给用户带来困扰。

3. 特征变换引入非线性性的常用方法

由于线性模型的建模能力较弱，因此我们需要考虑引入原始特征的非线性变换，常用的非线性变换方法包括：

人工交叉特征(包括交叉统计特征)
GBDT算法建模，并提取每个决策树的叶子节点（对应决策路径上的特征交叉）
DNN（如双塔模型、GNN等）抽取的用户embedding
FM模型提取到的交叉特征
等等

当前，后面几钟基于模型的方法一般都是基于非冷启动物品的行为样本训练出来的，训练好的模型用来对冷启动物品提取特征。

4. 可以考虑加入一维bias特征

由于LinUCB算法把每个候选物品都当做是MAB模型的一个arm，为每一个物品训练一个单独的模型，因此我们构建特征时主要关注用户侧特征、用户-物品交叉特征；一般情况下不需要物品侧的特征，因为这些特征对于对应的模型来说在每个样本中的值都是一样的。然而，我个人认为可以加一维bias特征，用来表示对物品的先验偏好。

由于，我们知道模型对全新的物品的预测跟特征向量的模（长度）正相关，因此，如果能够根据物品的内容属性特征来训练一个人气分模型，用模型预测的人气分作为arm对应模型的bias特征，则可以在初始状态选择人气分较高的物品优先展现，这样做可以让系统不至于从“冰点”开始探索。

五、超参数选择

特征的维数

尽量设计强特征，维数在保证算法效果的前提下不要太大，否则会给模型参数同步、大量候选物品的模型同时inference的过程带来较大的性能开销。

Disjoint vs Hybrid

在新物品集合变化频繁的场景推荐使用Hybrid模型，在新物品集合相当较稳定的时候推荐使用Disjoint模型。

下面是一个模拟测试的结果，在模拟训练的初期，共享参数的hybrid算法相比不共享参数的disjoint算法获得了更高的收益，然而随着实验的持续，disjoint算法最终能够获得更高的收益目标。这也就提示我们，如果我们面临的业务场景有源源不断的新物品加入，并且加入的频率比较高，那选择hybrid算法可能更加合适一些，毕竟每个新物品能获得的曝光机会少了，disjoint算法可能不能获得足够数量的样本使其收敛到较好的状态；而hybrid算法由于能够捕捉相似物品的一些共有特性，收敛速度更快。

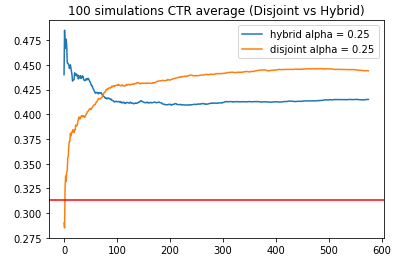
alpha参数

alpha参数用来平衡算法探索与利用，alpha越大，探索程度越大，反之，利用程度越大。建议当arm的集合越大时，alpha需要更小一些。

小毛驴