深度学习语义相似度系列：表示学习

深度学习语义相似度模型旨在学习输入$x$的一个好的特征表示，使得该特征表示能够捕捉到输入的本质结构，且能够促进后续的学习任务，如分类或聚类任务。一般地，我们用深度网络的某个中间层输出作为学习到的特征表示，基于该特征表示可以较方便地得到后续的分类结果，过程如下式所示，其中 $z=f(x,\theta) \in R^d$ 即为学习到的特征表示。

$$\require{AMScd} \begin{CD} x @>f(x,\theta)>> z(\theta) @>g(z)>> y \end{CD}$$

那么什么样的特征表示才是一个好的表示呢？其实，这个问题是和具体任务相关的，不同任务对特征表示的要求是不一样的，因而，我们不能期待在一个任务中有效的特征表示在另一个不同领域的任务上也同样有效。抛开具体任务不谈，原则上，我们期望特征表示既具有一定的信息量（informative），能够充分还原原始输入；又具有一定的区分性（discriminative），能够有效区别开不同类别的输入。从信息论的角度来说，期望能够在最小化原始输入与特征表示的互信息的同时最大化特征表示与目标类别的互信息，形式化如下：

$$max_{\theta \in \Theta} I(z(\theta), y)- \beta I(x, z(\theta))$$

其中，$\beta>0$，用来调节信息量与区分性的权重。

1. 语义相似度 vs 类别相似度

首先要解释一下标签相似度与语义相似度的区别。假设每段文本都表达了多重语义，那么语义相似度模型会判定两段语义重合度较高的文本是相似的，而标签相似度模型则要关注两段文本是否都提及了某种特定类型的语义，而不在乎这两段文本整体的语义重合度。举例说明如下：

1. 手机挂九游挂饰吊坠微信玉石玛瑙指环扣女款创意炸金花链短吊环
2. 玉石菩提手机扣指环挂绳短款手机挂饰挂件吊坠手机链短男女指环扣
3. 炸金花透视辅助 详情私聊
4. c 美诗美童田慧新款炸金花背心透视成人男款拉丁练习舞服 zq n01

语义相似度模型可能会判定文本1与文本2更相似，而标签相似度模型则会判定文本1与文本3更相似，因为它们有相同的风险标签：作弊造假。同样，标签相似度模型也会判定文本1和文本4是相似的，而语义相似度模型则可能会判定它俩不相似。

我们最终的目标是学习一个能够表示文本标签信息的embedding向量。学习到的向量空间需要能够很好地区分不同的风险类别，也就是说，相同类别的风险文本映射到向量空间中相近的位置，不同类别的风险在向量空间中的距离较远。

语义相似度关注整体语义，要求学习到的embedding向量能够尽可能还原原始输入；而标签相似度仅关注局部语义，既是否在预定义的标签维度上相似。定位不同，则解题思路也不同。语义相似度对应representation learning，而标签相似度对应的解决方案是metric learning。虽然两种技术思路有很大比例的交叉重叠，但是细微的不同可能会对业务效果产生蝴蝶效应般的影响。在风控领域，我们通常不管监管对象表达了多少正常的语义，我们只对监管对象是否触发了某种类型的违规敏感。我们的模型需要识别出隐藏在多种正常语义之下的违规风险语义。

2. 类别标签 vs 成对标签

提供给相似度模型学习的样本标签通常有两种类型，分别是成对标签（pair-wise labels）与类别标签（class-level labels）。例如，做人脸识别时，若样本是一对人脸图像，标签为是否为同一人的0/1标签，则这样的标签称之为成对标签。广义上讲，三元组、四元组标签都属于成对标签。同样是人脸识别场景，若样本为一个人脸图像，标签为该人脸的id（建模为一个超级大规模的分类模型），则这样的标签体系称之为类别标签。

通常情况下，类别标签使用分类损失函数，如softmax cross entropy loss或其变种，来优化样本特征表示与类别权重向量之间的相似度。成对标签使用某种度量损失函数来优化样本之间的相似度。具体可使用的损失函数可以参考这篇文章《深度度量学习中的损失函数》。这两种损失函数本质上并没有根本区别，它们都在尝试最小化类间相似度（between-class similarity）的同时最大化类内相似度(within-class similarity)。

3. Softmax loss vs Triplet loss

损失函数指导模型如何学习。Triplet loss是Metric Learning领域经典的损失函数，最初用在人脸识别领域。该loss函数要求样本由三元组(anchor, positive, negative)组成，其中positive的样本与anchor样本有相同的类标签，且与negative的样本有不同的类标签。如下图所示：

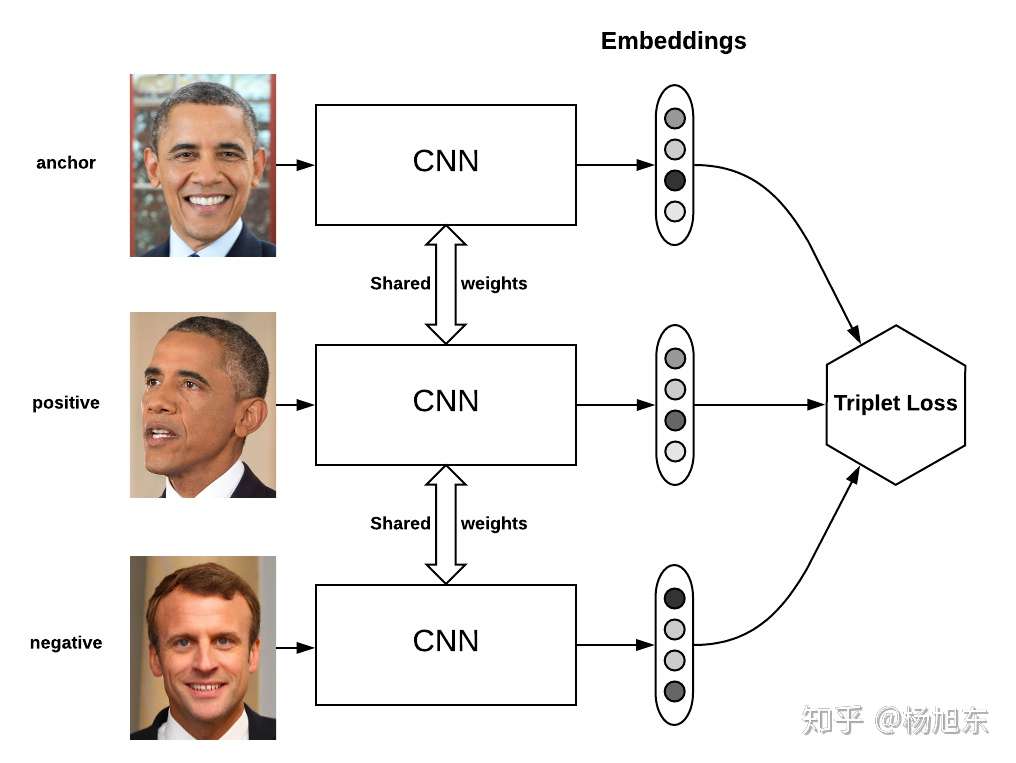
Triplet loss要求negative样本与anchor样本之间的距离比positive样本与anchor之间的距离至少大margin，定义如下：

$$\mathcal{L} = max(d(a, p) - d(a, n) + margin, 0)$$

最近的研究表明，通过为分类设计的softmax loss训练得到的embedding向量在需要计算样本距离的任务中表现也很好，例如可以用大规模softmax分类来训练人脸识别模型。进一步的研究表明，softmax loss与平滑版的triplet loss是等价的。网络最后一个全连接层的权重为每个类赋予了一个类中心embedding向量，而网络最后一个隐层的值即为样本的embedding向量。Softmax loss相当于是定义在（原始样本，样本类中心，另一个类的类中兴）三元组上的triplet loss，因此要求原始样本与其对应的类中心的距离比与另外任意一个类中心的距离都要小。要得到好的embedding表示，我的观察是softmax loss适用于类内方差较小且有大量类别的场景，比如人脸识别。然而，大规模softmax分类（如千万量级的类别）在工程实现上是非常困难的，受制于gpu显存大小的限制，需要实现数据并行加模型并行的分布式训练模型。相比softmax loss，triplet loss可以方便地训练大规模数据集，不受显存大小的限制；triplet loss的缺点是过于关注局部，导致对样本的构建要求很高且收敛时间长。

4. Circle Loss

除了《深度度量学习中的损失函数》中提到的损失函数，还可以使用最近提出的circle loss，该损失函数在多个场景下被验证效果很好。

大多数的损失函数，包括triplet loss 和softmax loss损失函数，都是使类间相似性 $s_n$ 和类内相似性 $s_p$ 嵌入到一个相似性对，并且去最小化$(s_n-s_p)$。这样的优化方式是不够灵活的，因为其对每一个单一相似性分数的惩罚强度是相等的。Circle loss提出如果一个相似性得分远离最优的中心，那么其应该被更多的关注(即惩罚)。基于这个目的，circle loss重新加权那些欠优化的相似性得分。

Circle loss对类别标签和成对标签使用统一的视角。已知在特征空间的一个单个样例 $x$，假设有 $K$ 个类内相似性得分$ \{s_p^i\}(i=1,2,\cdots,K)$， $L$ 个类间相似性得分$ \{s_n^j\}(j=1,2,\cdots,L) $。

一个统一视角的表示学习损失函数为

$$\begin{align*} L_{uni} &= log[1 + \sum_{i=1}^K \sum_{j=1}^L exp(\gamma(s_n^j - s_p^i + m))] \\ &= log[1+\sum_{j=1}^L exp(\gamma(s_n^j + m)) \sum_{i=1}^K exp(\gamma(- s_p^i))] \end{align*}$$

对上式简单的修改可以得到triplet loss和softmax loss。

自适应加权(Self-placed Weighting)

考虑一种更灵活的优化策略去允许每个相似性得分根据其优化状态去选择优化权重。首先忽略掉公式[公式]中阈值(margin) [公式] ，将其转换为Circle loss:

$$\begin{align*} L_{circle} &= log[1 + \sum_{i=1}^K \sum_{j=1}^L exp(\gamma(\alpha_n^j s_n^j - \alpha_p^i s_p^i))] \\ &= log[1+\sum_{j=1}^L exp(\gamma\alpha_n^js_n^j) \sum_{i=1}^K exp(-\gamma \alpha_p^i s_p^i)] \end{align*}$$

在训练期间 $ (\alpha_n^j s_n^j - \alpha_p^i s_p^i) $ 反向传播时对 $s_n^j(s_p^i)$ 的梯度分别乘上 $\alpha_n(\alpha_p)$ 。假设 $s_p^i$ 最优的状态是$O_p$ ， $s_n^j$ 最优的状态是 $O_n$ ，其中( $O_n < O_p$ )。当一个相似性分数远离他的最优点时(即 $s_n^j$ 远离 $O_n$, $s_p^i$ 远离$O_p$)，这时其应该获得更大的权重因子，以便于更好优化使相似性分数趋近于最优值。所以 $\alpha_n^j$ 和 $\alpha_p^i$ 定义为：

$$\begin{cases} \alpha_p^i = [O_p-s_p^i]_+ \\ \alpha_n^j = [s_n^j - O_n]_+ \end{cases}$$

其中，$[\cdot]_+=max(0,\cdot)$，表示在0截断，确保函数值为非负数。

Circle loss中的自适应加权，类似于focal loss。

类内和类间的阈值(With-in class and Between-class Margins)

在以往的损失函数中通过添加一个阈值 $m$ 去优化 $(s_n-s_p)$ ，因为 $s_n$ 和 $-s_p$ 是对称的，在 $s_n$ 处添加一个正的 $m$ 等价于在 $s_p$ 处添加一个负的 $m$。在Circle loss中 $s_n$ 和 $s_p$ 是不对称的。所以其对 $s_n$ 和 $s_p$ 分别需要一个阈值(margin)，用公式表示如下：

$$L_{circle}=log[1 + \sum_{j=1}^L exp(\gamma \alpha_n^j(s_n^j-\Delta_n)) \sum_{i=1}^K exp(-\gamma \alpha_p^i(s_p^i - \Delta_p))]$$

其中，$\Delta_n$和$\Delta_p$分别为类间和类内的阈值。

为了减少超参数，设置 $ O_p=1+m, O_n=-m, \Delta_p=1-m, \Delta_n=m $。

5. 总结

本文总结了表示学习领域的一些基本概念和常用的损失函数。包括Circle loss在内的常用损失函数的源码可以关注微信工资号：“算法工程师的进阶之路”，回 复 “损失函数”获取。